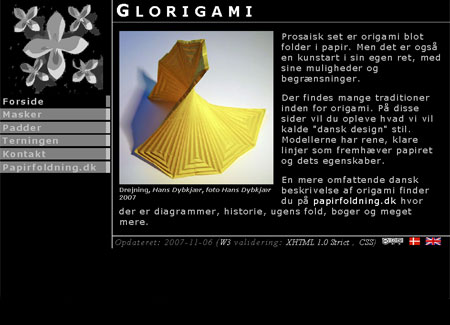
Phi og det gyldne rektangel
Det gyldne rektangel har sidelængder i forholdet phi:1 hvor phi = 1.6180 er det gyldne snit. Det kan konstrueres ganske enkelt ud fra ethvert rektangel. Efter foldesekvensen bringer vi et bevis for konstruktionens korrekthed.
Bevis
Konstruktion af det gyldne rektangel,
Hans Dybkjær,
2008
Beviset følger ganske tæt beviset gengivet i Kasaharas Origami Omnibus, 1988.
 Det gyldne rektangel er defineret ved: a/b = b/(a - b), hvilket giver a/b = (1 + kvr(5))/2 hvor kvr står for kvadratrod. Afrundet er det 1,6180, og forholdet synes fundamentalt i naturen, lige fra placeringen af frø i solsikker, over sneglehusvækst og bier, og til mængden af efterkommere.
Det gyldne rektangel er defineret ved: a/b = b/(a - b), hvilket giver a/b = (1 + kvr(5))/2 hvor kvr står for kvadratrod. Afrundet er det 1,6180, og forholdet synes fundamentalt i naturen, lige fra placeringen af frø i solsikker, over sneglehusvækst og bier, og til mængden af efterkommere. En vigtig egenskab er at den er sin egen inverse minus en. Derfor kan det gyldne rektangel også konstrueres ved at have langside 1 og kortside phi - 1.
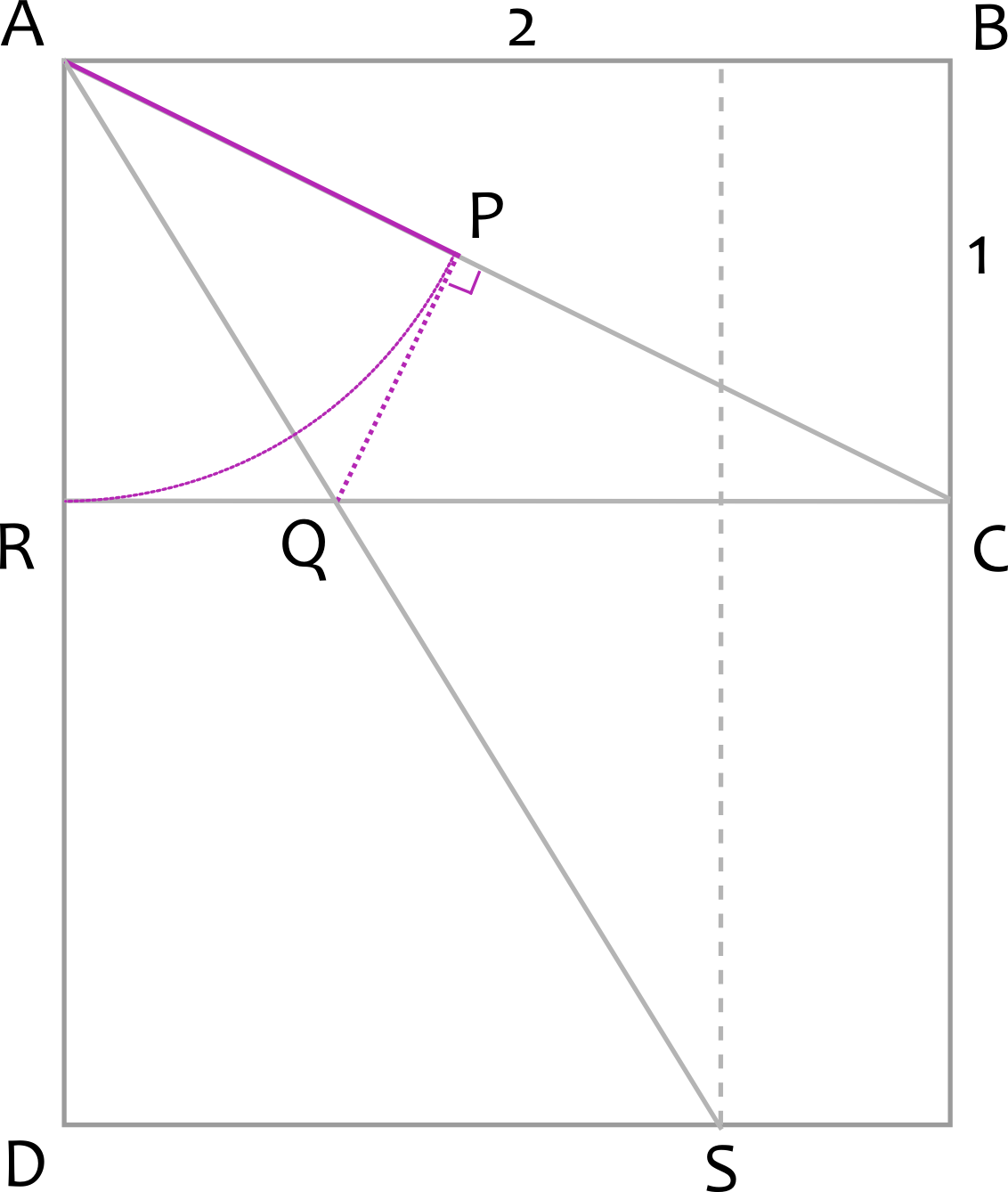
En vigtig egenskab er at den er sin egen inverse minus en. Derfor kan det gyldne rektangel også konstrueres ved at have langside 1 og kortside phi - 1. 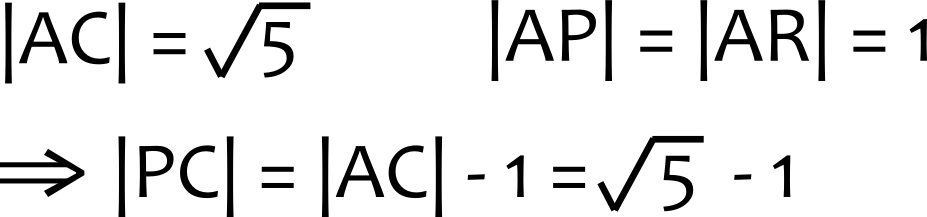 Det afgørende i konstruktionen er at få afmærket et 2x1 rektangel foroven, se tegningen til højre. Så siger Pythagoras at stykket |AC| er kvr(5), og vi får stykket |PC| til kvr(5) - 1.
Det afgørende i konstruktionen er at få afmærket et 2x1 rektangel foroven, se tegningen til højre. Så siger Pythagoras at stykket |AC| er kvr(5), og vi får stykket |PC| til kvr(5) - 1. De to trekanter ABC og CPQ har samme vinkler og er derfor ækvivalente.
De to trekanter ABC og CPQ har samme vinkler og er derfor ækvivalente.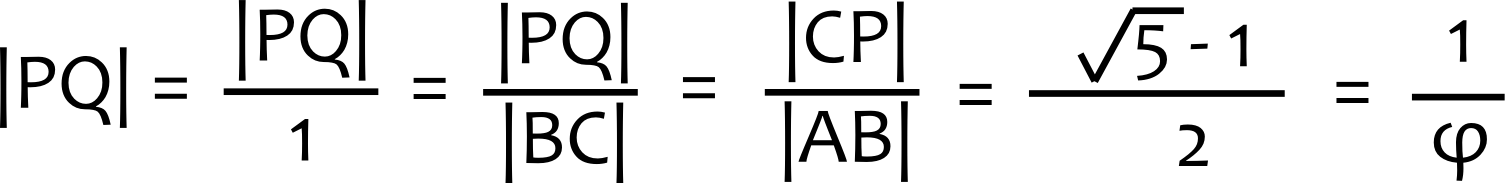 Stykket |PQ| kan nu beregnes til 1/phi. Eftersom |AP| er 1 og eftersom de to linjestykker ligger vinkelret, er de sider i et gyldent rektangel, jf. (2) ovenfor.
Stykket |PQ| kan nu beregnes til 1/phi. Eftersom |AP| er 1 og eftersom de to linjestykker ligger vinkelret, er de sider i et gyldent rektangel, jf. (2) ovenfor. Eftersom trekant APQ er ækvivalent med trekant ADS, er de to vinkelrette sider i denne trekant også sider i et gyldent rektangel.
Eftersom trekant APQ er ækvivalent med trekant ADS, er de to vinkelrette sider i denne trekant også sider i et gyldent rektangel.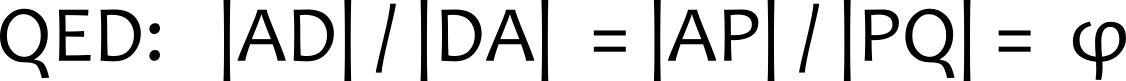 Ved at skære vinkelret af i S, har vi dermed konstrueret et gyldent rektangel. Det kan ske at S ligger på siden i stedet for i bunden. I så fald er den vinkelrette afskæring blot vandret i stedet for lodret, konstruktionen er stadig korrekt.
Ved at skære vinkelret af i S, har vi dermed konstrueret et gyldent rektangel. Det kan ske at S ligger på siden i stedet for i bunden. I så fald er den vinkelrette afskæring blot vandret i stedet for lodret, konstruktionen er stadig korrekt.